Vitodens-300W Integralschwellwert zur Abschaltung des Brenners

[meinereiner]

• Hallo,
  
  ich würde gerne verstehen, was diese beiden Parameter so darstellen.
  
  - 1606.0 "Brenner-Mindestpausezeit"
                 0 Brenner-Mindestpausezeit fest eingestellt (wie lange ist hier FEST??????)
  - 1606.4 "Integralschwellwert zur Abschaltung des Brenners"

        Integral ist für mich ein Begriff aus der Mathematik/Flächenberechnung. Kennt jemand die                Funktion welcher Fläche auch immer? Was passiert, wenn die Fläche größer/kleiner wird????

Danke

Gruß Ralf

[har1]

Du hast die Funktion eigentlich schon erklärt.

1606.0 "Brenner-Mindestpausezeit"  : entweder stellst du eine feste Zeit(Größe kenne ich nicht) ein ,   oder du benutzt den Parameter 1606.4 "Integralschwellwert zur Abschaltung des Brenners" – die bessere Wahl.

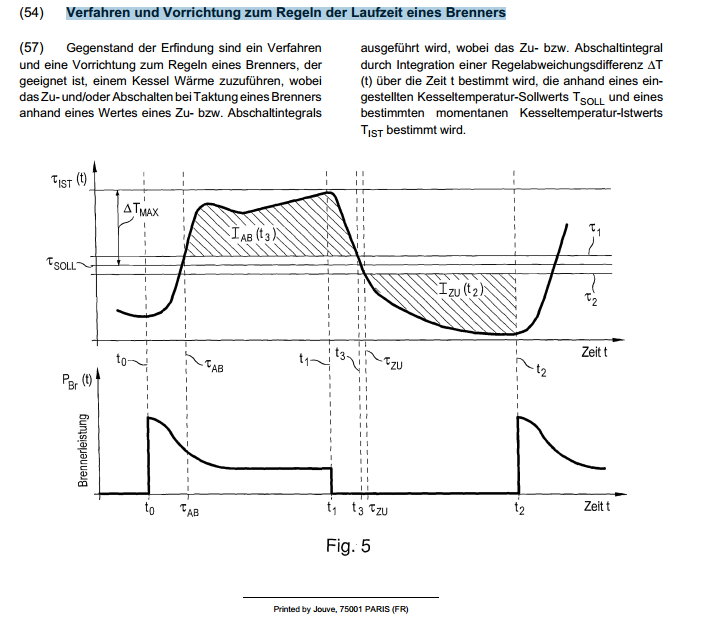
Der Parameter 1606.4 "Integralschwellwert zur Abschaltung des Brenners" stellt quasi eine Fläche (aus Temp. (über Temp. Anforderung) und Zeit) dar. Mit dem Wert stellst du einerseits den Abschaltpunkt (zu warm), aber auch den Einschaltpunkt (nach Abkühlung) ein.

Wie die Einstellung vom 1606.4 konkret ist , hängt vom Haus, Gewohnheit, Temp.Gefühl…….ab.

Ich habe den 1606.4 auf 1500 stehen. – Für mich!

Siehe Bild von Viessmann

[Dreman · Accepted solution]

Oder hier im Original mit zusätzlichen Vermutungen (vorletzter Beitrag) 😉.

[meinereiner]

Danke euch 2 🙂
Ich habs verstanden 😁

Ein schönes Wochenende

Gruß Ralf

[Klaus16]

Vielleicht eine etwas theoretische Frage. Wäre es nicht besser die Integration von delta t über den Volumenstrom zu ermitteln statt über die Zeit?

Gruß

[har1]

Das ist eine gute Frage. Funktionieren würde die Benutzung des Volumenstromes bestimmt.

Ob es besser wäre, kann ich nicht beantworten.

Es könnte sein, dass die Zeit einfacher zu benutzen ist als der Volumenstrom, der vielleicht variieren kann, und dann auch noch umgerechnet werden muss.

Vielleicht hat Viessmann auch nur den einfachen Weg gewählt, oder ein Anderer hält das betreffende Patent.

Das Patent von Viessmann bezieht nur auf die Zeitbenutzung.

[Dreman]

Nur interessehalber, warum Volumenstrom? Letztendlich ist doch das Verfahren nichts anderes als eine 'intelligente' symmetrische Hysterese für die Soll-Vorlauftemperatur: je größer der eingestellte Wert, umso später (Integration über der Zeit) schaltet der Brenner ab. Und je größer der eingestellte Wert, umso länger (Integration über der Zeit) pausiert anschließend der Brenner.

[Klaus16]

Macht wahrscheinlich wirklich keinen Unterschied.

[Dreman]

Wenn das so ist, dann erkläre doch bitte mal in mehr als 5 Wörtern, warum das so ist. Ich würde es einfach gerne verstehen 😉.

[Klaus16]

Gerne

Ich habe mich etwas unglücklich ausgedrückt. Gemeint hatte ich, dass man über das Volumen (des Volumenstroms) integriert.

Die X-Achse wäre dann das Volumen, dass dann vom Zeitpunkt t0 zunimmt, bis zum Zeitpunkt tx.

Die y-Achse ist weiterhin die Temperatur.

Rein mathematisch betrachten hätte das Integral zwar eine andere Fläche, das gilt allerdings nicht nur für die Integralfläche wenn der Brenner an ist, sondern auch für die Integralfläche, wenn der Brenner aus ist.

Deswegenglaube ich inzwischen, wie schon geschrieben, dass es keinen Unterschied macht.

Gruß

[Dreman]

Die x-Achse ist also gleichzeitig Volumen und Zeit? Und die y-Achse ist nach wie vor die (Vorlauf-)Temperatur, obwohl über den Volumenstrom integriert wird? Sorry, das ist mir zu hoch, ich bin raus 😉.

[Klaus16]

Opps, schon wieder unglücklich ausgedrückt. Die X-Achse geht natürlich von V0 bis Vx

[Dreman]

Dann kann die y-Achse keine Temperatur darstellen. Überleg dir deine Theorie nochmal in Ruhe 😉.

[meinereiner]

Hallo Klaus,

du willst ja letztendlich den Durchfluss über die Zeit darstellen. Wenn du dann noch die Temperatur einbringen möchte, dann geht das nicht in einem Kartesischen Diagramm. Das kennt nämlich nur 2 Dimensionen. Abszisse (X) für die Zeit und entweder den Sollwert auf der Ordinate (Y) oder alternativ den Durchfluss.

Gruß Ralf